
| КрасносельскийКонстантинКонстантинович
|

 Компьютер и программы
Компьютер и программы

 WEB-дизайн
WEB-дизайн

 Литература и поэзия
Литература и поэзия

 Гуманитарные науки
Гуманитарные науки

 Мастерская
Мастерская
 Хронология материалов
Хронология материалов
 Обращение к посетителям
Обращение к посетителям
 Скачать шрифты
Скачать шрифты
 Скачать рефераты
Скачать рефераты
 Создание web сайта на заказ
Создание web сайта на заказ
 Создание веб сайтов (цены)
Создание веб сайтов (цены)
 Веб-сайты, созданные мной (потенциальным заказчикам)
Веб-сайты, созданные мной (потенциальным заказчикам)
 Полезные ссылки
Полезные ссылки
 Об авторе
Об авторе
 Статистика сайта
Статистика сайта
 Показать фреймы
Показать фреймы
ТаблицейБлоками.Альтернативная логика: Умозаключения |
Последняя модификация: 10.08.2014 г
Страница загружена с адреса: http://humanus.site3k.ru/logic/alt/chapter4.html

Глава 4. Умозаключения
Умозаключения.
Умозаключение – форма мышления, включающая посылки (исходные суждения), заключение и логическую связь между ними, посредством которой, не обращаясь к органам чувств, из одного или нескольких суждений можно получить новые знания, могущие быть истинными, логически необходимыми, или только правдоподобными, с некоторой долей вероятности следующие из посылок. При этом если из условия вытекает следствие, условие является достаточным, если условие само вытекает из следствия – условие является необходимым. Умозаключения делятся на дедуктивные, индуктивные и, умозаключения по аналогии.
При соблюдении правил умозаключения логическое следствие из посылок не может быть ложным, несмотря на возможную логическую неочевидность или даже, кажущуюся невероятность. Так, например, из истинных посылок «Все углероды горючи» (углерод – С – высокоактивный, легко окисляющийся химический элемент) и «Алмаз – углерод» (в его кристаллической структуре), получается, на первый взгляд абсурдное, но, тем не менее, истинное следствие: «Алмаз горюч», – для проверки которого не требуется проведения эксперимента по сжиганию алмаза. Такое, заведомо истинное умозаключение, является дедуктивным.
Дедуктивные умозаключения
Дедуктивные умозаключения, опираясь на тот факт, что ничто частное не существует вне общего, выводят заключение из посылок по принципу необходимого логического следствия, определяющего что, следствие не может не быть, если есть достаточная для него причина (основание). Они дают достоверную информацию, поскольку используют лишь факторы, уже содержащиеся в посылках. И, если собранные вместе посылки приводят к необходимости нового суждения, то оно содержит информацию уже содержащуюся в них и не требующую дополнительных доказательств.
Дедуктивные умозаключения делятся на опосредованные – выводимые из нескольких посылок и непосредственные – выводимые из одной (умозаключение по квадрату и преобразование одиночных суждений).
Непосредственные дедуктивные умозаключения. Преобразование одиночных суждений.
Непосредственные дедуктивные умозаключения из одиночной посылки представляют собой простые категорические суждения существования или свойств. В зависимости от способа преобразования, делятся на преобразование по квадрату и преобразование одиночных суждений, в свою очередь делимое на обращение, превращение и противопоставление предикату.
Превращение, затрагивая все четыре типа категорических суждений (A, I, E, O) изменяют качество посылки, не меняя ее количественных показателей, ставя предикат нового суждения в противоположность предикату исходного. При этом, общеутвердительные суждения переходят (превращаются) в общеотрицательные и наоборот, а частноутвердительные в частноотрицательные (и наоборот). Что в математической записи имеет вид:
A → E; E → A; I → O; O → I
Причем, в суждениях E и I, при превращении речь о субъекте сменяется на речь о предикате, что позволяет представить субъект в новом ракурсе.
| A | Все S являются P Все S не являются не-P |
E | Ни одно S не является P Все P являются не-S |
| I | Некоторые S являются P Некоторые P не являются не-S |
O | Некоторые S не являются P Некоторые S являются не-P |
Обращение обращает предикат посылки в субъект заключения, а субъект в предикат. В зависимости от качества заключения бывает чистое, затрагивающее три типа суждений – A, E, I, – не меняющее количество, при условии что, ни субъект, ни предикат, в полном объеме, не являются лишь частью другого (например, не все преступления, являются неумышленными действиями и термин «преступление», в своем полном объеме не является лишь частью неумышленных действий)1, по схеме (A → A; E → E; I → I):
| A | Все S (и только S)являются P Все P (и только P) являются S |
E | Ни одно S не является P Ни одно P не являются S |
| I | Некоторые S являются P Некоторые P являются S |
O | Не дает истинных значений при чистом обращении |
И с ограничением, затрагивая два типа суждений – A и I – если один из терминов, в своем полном объеме является лишь частью другого (как углероды – лишь часть горючих веществ, а птицы – лишь часть яйцекладущих), по схеме (A → I; I → A):
| A | Все S являются P Некоторые P (и только P) являются S |
Сужение общеутвердительных суждений |
| I | Некоторые S (и только S) являются P Все P являются S |
Обобщение частноутвердительных суждений |
Противопоставление предикату, затрагивая три типа суждений – A, E, O – превращает субъект в предикат, а противоречащие предикату понятие (его антагонизм), в субъект, по сути, являясь результатом превращения с последующим обращением и, происходит по схеме (A → E; E → I; O → I):
| A | Все S являются P Ни одно не-P не являются S |
E | Ни одно S не является P Некоторые не-P являются S |
| I | Не дает значений |
O | Некоторые S не является P Некоторые не-P являются S |
Все виды преобразований одиночных суждений (непосредственных умозаключений) дают новую информацию, особенно интересную при противопоставлении предикату. Так, например, этим способом из суждения «Некоторые преступления не являются умышленными» получается «Некоторые неумышленные действия являются преступлениями».
Преобразование по квадрату.
Как уже говорилось, в логическом квадрате суждения A и E являются подчиняющими, а I и O подчиненными. Преобразования по квадрату, как и все, следующие за ним методы умозаключения, опираются на закон транзитивности, по которому из истинности подчиняющих суждений логически следует истинность суждений им подчиненных и ложность противоположных подчиненных суждений. Так, из истинности A следует истинность I и ложность O (A → I; A ≡O), а из истинности E следует истинность O и ложность I (E → O; E ≡I). Например, из истинности суждения «Все углероды горючи», логически следует что, и некоторые углероды (алмаз), горючи в том числе. Так же, истинность одного подчиняющего суждения указывает на ложность противопоставленного ему другого подчиняющего суждения (A →E; E →A), например, из истинности «Все углероды горючи», следует ложность суждения «Ни один углерод не горюч». Из истинности подчиненных суждений, следует ложность противоположных им подчиняющих (I →E; O →A), а из ложности подчиненных, ложность их подчиняющих (I →A; O →E). Таким образом, вся структура преобразований по квадрату сводится к следующим, легко усваиваемым формулам:

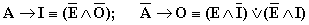
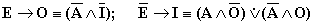
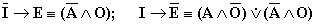
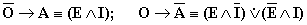
Из чего следует что в сложном разделительном суждении типа 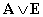 либо только одно суждение истинно, либо оба суждения ложны (например: «Либо все люди – негры (1), либо не один человек не негр (2)»), а в сложном разделительном суждении типа
либо только одно суждение истинно, либо оба суждения ложны (например: «Либо все люди – негры (1), либо не один человек не негр (2)»), а в сложном разделительном суждении типа 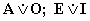 одно суждение обязательно истинно (например: «Либо все птицы летают (1), либо некоторые из них не летают (2)»). В сложном суждении типа
одно суждение обязательно истинно (например: «Либо все птицы летают (1), либо некоторые из них не летают (2)»). В сложном суждении типа 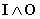 оба простых суждения могут быть одинаково истинными, хотя одно из них, может оказаться ложным («Некоторые люди счастливы (1), в то время, когда некоторые, несчастны (2)»).
оба простых суждения могут быть одинаково истинными, хотя одно из них, может оказаться ложным («Некоторые люди счастливы (1), в то время, когда некоторые, несчастны (2)»).
Но, не смотря на кажующуюся простоту, преобразование по квадрату дает много полезной информации. Например, частноутвердительное суждение «Существуют такие рыбы, которые не дышат легкими» (I) дает два прямых следствия:
- «Не верно что, все рыбы дышат легкими» (A).
- «Либо ни одна рыба не дышит легкими и неверно что, некоторые все же дышат ими (E
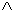 I), либо (
I), либо (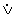 ) неверно что ни одна рыба не дышит легкими (E)». Второе (дезинъюнктивное следствие можно сократить, отбросив его средние члены и получить упрощенный вариант дезинъюнктивного заключения «Либо ни одна рыба не дышит легкими, либо некоторые, все же, дышат ими» (E
) неверно что ни одна рыба не дышит легкими (E)». Второе (дезинъюнктивное следствие можно сократить, отбросив его средние члены и получить упрощенный вариант дезинъюнктивного заключения «Либо ни одна рыба не дышит легкими, либо некоторые, все же, дышат ими» (E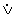 I).
I).
Еще более интересные следствия дает общеутвердительное суждение «Все углероды горючи», прямым следствием которого является горючесть алмаза. Подобные умозаключения обычно считаются силлогизмами и записываются в виде:
Все углероды горючи Алмаз – углерод Алмаз горюч |
Но, на самом деле, это ни что иное как переходное звено от преобразований по квадрату к настоящим силлогизмам, поскольку понятие «углероды» включает понятие «алмазы» и не требует дополнительных посылок («Все углероды горючи; некоторые углероды, в том числе и алмаз, горючи тоже»), в то время как настояшие силлогизмы без них не возможны.
< Глава 3 Глава 4 Глава 5. >
