
| КрасносельскийКонстантинКонстантинович
|

 Компьютер и программы
Компьютер и программы

 WEB-дизайн
WEB-дизайн

 Литература и поэзия
Литература и поэзия

 Гуманитарные науки
Гуманитарные науки

 Мастерская
Мастерская
 Хронология материалов
Хронология материалов
 Обращение к посетителям
Обращение к посетителям
 Скачать шрифты
Скачать шрифты
 Скачать рефераты
Скачать рефераты
 Создание web сайта на заказ
Создание web сайта на заказ
 Создание веб сайтов (цены)
Создание веб сайтов (цены)
 Веб-сайты, созданные мной (потенциальным заказчикам)
Веб-сайты, созданные мной (потенциальным заказчикам)
 Полезные ссылки
Полезные ссылки
 Об авторе
Об авторе
 Статистика сайта
Статистика сайта
 Показать фреймы
Показать фреймы
ТаблицейБлоками.Альтернативная логика: Суждения (высказывания) |
Последняя модификация: 10.08.2014 г
Страница загружена с адреса: http://humanus.site3k.ru/logic/alt/chapter3.html

Глава 3. Суждения (высказывания)
- Суждение (высказывание).
- Простые суждения
- Сложные суждения.
- Сравнимость суждений
- Исчисление высказываний
- Правила формальной логики (отношения высказываний).
Суждение (высказывание).
Суждение – форма мышления, мысль, высказанная повествовательным предложением, могущая быть истинной или ложной. Побудительные или вопросительные предложения не содержат явных суждений, но могут иметь их в скрытой форме, проявляемой из контекста или в процессе осмысления. Например, вопрос «Можно ли доверять человеку, однажды уличенному во лжи?», содержит скрытое суждение «Человек, однажды уличенный во лжи, еще долго будет вызывать недоверие».
В зависимости от формы, (количества составных частей), как и обычные повествовательные предложения, суждения делятся на простые и сложные.
Простые суждения
Простые суждения затрагивают один фактор («Лень – это отвращение к деятельности и инициативе, особенно умственной») и состоят из субъекта (S) – предмета суждения о котором идет речь и, который суждение выдвигается на первый план, акцентируя на нем внимание и, предиката (P), дополняющего субъект. В предложении «Мыслить, значит видеть суть». Речь идет о мышлении, оно и есть субъект, предикат «видеть суть» лишь дополняет субъект. Но предложение можно перестроить, меняя его смысл и перенося акцент то на мышление, то на видение сути. В таком случае, будет меняться роль субъекта и предиката.
«Раскрывать мысль, значит, показывать суть» (SP).
«Показывать суть, значит, раскрывать мысль» (SP).
В приведенных примерах сначала субъектом является «раскрывать мысль», а предикатом «показывать суть (а не нагромождать всякую мешанину)», затем значение терминов меняется. Слово «значит», в данном примере, является логической связкой и не относится ни к субъекту, ни к предикату.
В зависимости от логического содержания, простые суждения делятся на ассерторические, констатирующие некий факт, не давая ему каких-либо дополнительных оценок и модальные. Ассерторические, в свою очередь, делятся на категорические, условные и разделительные.
Ассерторические суждения.
Простые категорические суждения существования, утверждающие что, признакам есть или нет места в реальном мире и имеющие структуру:
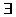 S есть P
S есть P
где 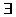 – квантор существования, означающий «по крайней мере, некоторые», «существуют такие» («некоторые преступления являются (есть) неумышленными»). Или:
– квантор существования, означающий «по крайней мере, некоторые», «существуют такие» («некоторые преступления являются (есть) неумышленными»). Или:
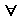 S есть P
S есть P
где 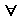 – квантор общности, означающий «все», «ни один».
– квантор общности, означающий «все», «ни один».
Простые категорические суждения свойств, утверждающие наличие или отсутствие свойств у какого-либо объекта и имеющие ту же структуру.
Категорические суждения существования и свойств являются самыми простыми и вместе с тем, основными видами суждений. Они делятся на:
A – Общеутвердительные: Все S являются P.
I – Частноутвердительные: По крайней мере, некоторые S являются P.
E – Общеотрицательные: Все (ни одни) S не являются P.
O – Частноотрицательные: По крайней мере, некоторые S не являются P.
Разделительные (дизинъюнктивные) суждения демонстрируют наличие (не строгое разделение) или необходимость (строгое разделение) выбора между несколькими альтернативами. При этом, в строгоразделительном суждении истинной (приемлемой) может быть только одна из альтернатив, а в нестрогой – одна или несколько. Нестрогое разделение обычно обозначается разделительной связкой (союзом) «или», стоящей между ее членами («Я излагаю или пишу») и обозначается знаком V. Строгое разделение, зачастую, содержит союз «или» перед каждым из членов («Это или закономерность природы, или случайность»), чтобы указать на необходимость выбора чего-то одного, но может ограничиваться и одной «или» между членами, особенно если один из них – отрицание другого. Хотя и в таких случаях, подчеркивая принципиальность вопроса, может применяться дважды: («Справедливость или есть, или ее нет»). Обозначается строгое разделение знаком 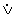 (c точкой над V).
(c точкой над V).
Условные (импликационные) суждения обозначаются знаком →. Они указывают на взаимосвязь между явлениями и строятся с помощью фактических связок «если… то», при этом причина (основание, антецедент) расположена после слова «если», а следствие (заключение, консеквент), после слова «то». Если же связка составлена без слова «то», по схеме «… если …», то заключение находится перед словом «если».
Категорические суждения отношений, утверждающие наличие или отсутствие между факторами определенных отношений, имея структуру S R P («Метр длиннее фута»), являются переходной формой мышления от ассерторических суждений к модальным.
Модальные суждения.
В отличие от ассерторических, просто констатирующих факт, модальные суждения выражают характер связи субъекта и предиката в простых суждениях и характер связи между частями сложных суждений, давая им оценку: Всегда, хорошо, вероятно, доказано и т. д. Их структура: M (S есть P). Например: «Не может стол иметь форму шара» (или «Не может быть что, стол имеет форму шара»), то есть, модальный оператор «M» просто добавляется к ассерторическому суждению («Стол имеет форму шара»), хотя иногда для этого требуются смена склонений или другие коррективы.
Модальная логика имеет несколько общих особенностей:
Необходимость означает невозможность отрицания.
Возможно означает «неверно, что необходимо».
Случайность означает возможность, как утверждения, так и отрицания.
Логически необходимое всегда истинно (что позволяет строить дедуктивные умозаключения), но не наоборот.
Истинность необязательно логически необходима, но всегда логически возможна (что позволяет строить индуктивные умозаключения), но не наоборот, поскольку логика не исключает лжи. И тем не менее:
Логически невозможное – обязательно лживо.
Физически необходимо то, отрицание чего нарушает законы природы. Физически необходимое всегда истинно.
В модальной логике имеются так же особенности логики оценок:
Хорошо лишь то, противоположное чему плохо (например, иметь машину хорошо лишь для того, кто в ней нуждается, иному она безразлична, но, вероятно, хороши вырученные за нее деньги).
То, что нарушает закон непротиворечия, не может иметь одну оценку.
К модальным суждениям можно отнести и внешнеотрицательные (опровергающие) суждения, например, опровергающее суждение «Неверно что, машина – роскошь», сходно модальному «Не может быть что, машина – роскошь», хотя в первом случае категорически утверждается ложность суждения, а во втором, его истинность оценивается как, маловероятная.
Сложные суждения.
Сложные суждения состоят из ряда простых («Человек не стремится к тому, во что не верит и, любой энтузиазм, не подкрепляясь реальными достижениями, постепенно угасает»), каждое из которых в математической логике обозначается латинскими буквами (A, B, C, D… a, b, c, d…). В зависимости от способа образования различают конъюнктивные, дизинъюнктивные, импликационные, эквивалентные и отрицательные.
Дизинъюнктивные суждения образуются с помощью разделительных (дизинъюнктивных) логических связок аналогичных союзу «или». Подобно простым разделительным суждениям бывают нестрогими (нестрогая дизинъюнкция), члены которой допускают совместное сосуществование (толи…, толи…), записывающимися a V b; и строгими (Строгая дизинъюнкция) члены которой исключают друг друга (либо одно, либо другое), записывающимися a 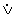 b (с точкой над V).
b (с точкой над V).
Импликационные суждения образуются с помощью импликации, эквивалентной союзу «если …, то» и записываются a → b или a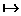 b, хотя в естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.
b, хотя в естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.
Конъюнктивные суждения образуются с помощью логических связок сочетания (конъюнкции) эквивалентной запятой или союзам «и», «а», «но», «да», «хотя», «который», «зато» и другим, обозначаемых знаком «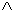 ». Что в математической логике записывается как (a
». Что в математической логике записывается как (a 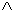 b).
b).
Эквивалентные суждения указывают на тождественность частей суждения друг другу (проводят между ними знак равенства). Помимо определений, поясняющих какой-либо термин, могут быть представлены суждениями, соединенными союзами «если только», «необходимо», «достаточно» (например: «Чтобы число делилось на 3, достаточно чтобы, сумма цифр, его составляющих, делилась на 3»), и записывается a ≡
b; a ↔ b; a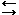 b (у разных математиков по-разному, хотя математический знак тождества все-таки ≡).
b (у разных математиков по-разному, хотя математический знак тождества все-таки ≡).
Отрицательные суждения строятся с помощью связок «не» и записываются либо a ~ b, либо a 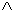 b при внутреннем отрицании типа «машина не роскошь», и с помощью черты над всем суждением при внешнем отрицании (опровержении) «не верно что …» (a
b при внутреннем отрицании типа «машина не роскошь», и с помощью черты над всем суждением при внешнем отрицании (опровержении) «не верно что …» (a 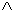 b).
b).
Сравнимость суждений
Помимо всего прочего, суждения делятся на сравнимые, имеющие общий субъект или предикат и несравнимые, не имеющие между собой ничего общего. В свою очередь, сравнимые делятся на совместимые, полностью или частично выражающие одну и ту же мысль и, несовместимые, если из истинности одного из них необходимо следует ложность другого (при сопоставлении таких суждений нарушается закон непротиворечия). Отношение по истинности между суждениями, сравнимыми через субъекты отображается логическим квадратом.
Логический квадрат лежит в основе всех умозаключений и представляет собой сочетание символов A, I, E, O означающих определенный тип категорических высказываний.
A – Общеутвердительные: Все S являются P.
I – Частноутвердительные: По крайней мере, некоторые S являются P.
E – Общеотрицательные: Все (ни одни) S не являются P.
O – Частноотрицательные: По крайней мере, некоторые S не являются P.
Из них общеутвердительные и общеотрицательные являются подчиняющими, а частноутвердительные и частноотрицательные – подчиненными.

Суждения A и E противопоставлены друг другу;
Суждения I и O противоположны;
Суждения, расположенные по диагонали – противоречивы.
Противоречивые и противопоставленные суждения ни в коем случае не могут быть одновременно истинными. Противоположные суждения могут быть или не быть одновременно истинными, но, по крайней мере, истинным должно быть одно из них.
Закон транзитивности обобщает логический квадрат, становясь основой всех непосредственных умозаключений и, определяет что, из истинности подчиняющих суждений логически следует истинность суждений им подчиненных и ложность противоположных подчиненных суждений.
Исчисление высказываний
Для верификации (проверки) истинности высказываний формальная логика дублируется математической путем составления всевозможных таблиц. Например, высказывание «a» и его отрицание «не-a» дает таблицу истинности:
| a | a |
|---|---|
| И | Л |
| Л | И |
Где «И» означает «истина», «Л» – «ложь».
Означающую что, если «a» истинно, то «a» ложно и наоборот.
В общем случае таблица составляется таким образом: Под последней частью высказывания (здесь «b») пишется друг за другом И, Л, И, Л, … и т. д., в предыдущем столбце, количество идущих подряд оценок удваивается (И, И, Л, Л, … и т. д.). И так в каждом предыдущем (если они есть) одинаковых оценок, идущих подряд в два раза больше чем в следующем. Количество строк определяется отношением Z=2n, где n – количество переменных (в данном случае два: «a» и «b»). Таким образом учитываются все возможные сочетания истинности и ложности. Простое составление (конъюнкция 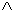 ) a и b истинно, если истинны обе составных части a и b. Поэтому во второй строке третьего столбца ставится «И». Подобные операции проделываются и дальше. Таблица позволяет определить что, сочетание (конъюнкция) истинно, когда все его части истины; строгое разделение (дизинъюнкция) – когда истинна только одна; нестрогое – когда истинна хотя бы одна и т. д. Существуют тождественно-истинные формулы, при любом значении переменных дающие истинные значения. Эти формулы являются правилами формальной логики.
) a и b истинно, если истинны обе составных части a и b. Поэтому во второй строке третьего столбца ставится «И». Подобные операции проделываются и дальше. Таблица позволяет определить что, сочетание (конъюнкция) истинно, когда все его части истины; строгое разделение (дизинъюнкция) – когда истинна только одна; нестрогое – когда истинна хотя бы одна и т. д. Существуют тождественно-истинные формулы, при любом значении переменных дающие истинные значения. Эти формулы являются правилами формальной логики.
| a | b | a 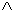 b b | a V b | a 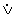 b b | a → b | a ≡ b
| И | И | И | И | Л | И | И
| И | Л | Л | И | И | Л | Л
| Л | И | Л | И | И | И | Л
| Л | Л | Л | Л | Л | И | И
| |
|---|
Исчислению подлежат все высказывания, как простые, так и сложные.
Правила формальной логики (отношения высказываний).
Правило коммуникации.
В логике высказываний конъюнктивные выражения, кроме выражений, учитывающих временную последовательность событий, подчиняются правилу коммутативности (коммуникации), позволяющему менять части высказывания местами. Можно, например, сказать: «Верить и ждать», или вместо этого сказать «Ждать и верить», поскольку события происходят одновременно. Но если вместо: «Она вышла замуж и родила ребенка», сказать «Она родила ребенка и вышла замуж», то произойдет смена временной последовательности событий и причинно-следственных связей, получится что, рождение ребенка предшествовало замужеству, что оно и стало его причиной. Совершать такие метаморфозы – значит нарушать принципы правильного мышления.
В целом же, правило коммуникации устанавливает следующие отношения:
(a 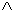 b) ≡ (b
b) ≡ (b 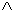 a); (a V b) ≡ (b V a)
a); (a V b) ≡ (b V a)
В конъюнкции и дизинъюнкции перестановка переменных не меняет смысла высказывания.
В логике отношений и модальной логике данное правило требует небольшого дополнения. Нельзя, например, вместо «Москва восточнее Парижа» (a R b) сказать «Париж восточнее Москвы» (b R a), нельзя даже сказать «Париж не восточнее Москвы» (b R a), поскольку это означает что, Париж может находиться как западнее Москвы, так и на одном меридиане с ней и, даже, в центре Москвы, что не предусматривалось первым утверждением. Эквивалентным будет лишь «Париж западнее Москвы», поскольку в логике отношений и модальной логике эквивалентация коммуникации происходит только путем антагонизации (подбора связки противоположной по смыслу), а простое введение отрицания сводит отношение к возможно безразличному.
Таким образом, на правиле коммуникации четко прослеживается общность суждений с отношениями и модальных суждений и легко заметно что, суждения с отношениями являются переходной формой от ассерторических суждений к модальным.
Правило эквивалентности.
Тесно связанное с правилом коммуникации, оно устанавливает эквивалентность между высказываниями:
- Сочетание (конъюнкция) утверждений эквивалентно (равносильно) опровержению неопределенности (дизинъюнкции) отрицаний («Он толстый и короткий: не верно что, он не толстый или что, он не короткий» a
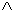 b ≡
b ≡ 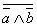 ); а сочетание отрицаний эквивалентно опровержению неопределенности утверждений («Он не толстый и не короткий: неверно что, он толстый или что, он короткий» a
); а сочетание отрицаний эквивалентно опровержению неопределенности утверждений («Он не толстый и не короткий: неверно что, он толстый или что, он короткий» a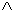 b ≡
b ≡ 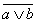 ).
).
- Неопределенность утверждений эквивалентна опровержению сочетания отрицаний («Он или толстый, или короткий: неверно что, он и не толстый, и не короткий» a V b ≡
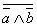 ); а неопределенность отрицаний эквивалентна опровержению сочетания утверждений («Он не толстый или не короткий: не верно что, он и толстый, и короткий» a V b ≡
); а неопределенность отрицаний эквивалентна опровержению сочетания утверждений («Он не толстый или не короткий: не верно что, он и толстый, и короткий» a V b ≡  ).
).
- Опровержение сочетания утверждений эквивалентно неопределенности отрицаний («Неверно что, он толстый и короткий: он, по крайней мере, или не толстый, или не короткий»
 ≡
≡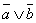 ); а опровержение неопределенности утверждений эквивалентно сочетанию отрицаний («Не верно что, он толстый или короткий: он и не толстый и не короткий»
); а опровержение неопределенности утверждений эквивалентно сочетанию отрицаний («Не верно что, он толстый или короткий: он и не толстый и не короткий» 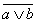 ≡
≡ 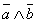 ).
).
- Условность (импликация) эквивалентна неопределенности следствия при отрицании причины и отрицанию причины при отрицании следствия (строгой дизинъюнкции отрицания одного и утверждения другого) – «Если он толстый, то значит короткий: или он короткий, или он не толстый»
 ≡
≡  ; и наоборот
; и наоборот  ≡
≡ ; а ее отрицание эквивалентно отрицанию следствия при наличии причины («Не верно что, если он толстый, то значит короткий: он толстый, но совсем не короткий»
; а ее отрицание эквивалентно отрицанию следствия при наличии причины («Не верно что, если он толстый, то значит короткий: он толстый, но совсем не короткий»  ≡
≡ 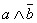 и наоборот
и наоборот 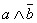 ≡
≡  ).
).
- Причина вызывающая несколько следствий имеет несколько эквивалентных формулировок (
 )
)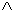 (
(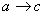 )≡
)≡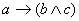 и наоборот
и наоборот 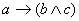 ≡(
≡( )
)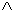 (
(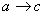 )
)
- Если различные причины имеют одинаковые следствия, это может быть представлено так: (
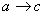 )
)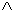
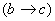 ≡
≡ – Разные причины с общим следствием эквивалентны неопределенности причины вызвавшей это следствие. Обратное допустимо с некоторыми оговорками: если мы предпологаем что, следствие вызвано одной из причин, значит мы допускаем что, каждая из этих причин способна вызвать данное следствие
– Разные причины с общим следствием эквивалентны неопределенности причины вызвавшей это следствие. Обратное допустимо с некоторыми оговорками: если мы предпологаем что, следствие вызвано одной из причин, значит мы допускаем что, каждая из этих причин способна вызвать данное следствие  ≡(
≡(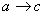 )
)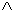
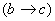 , чего на деле может и не быть.
, чего на деле может и не быть.
- Цепь причин, последовательно ведущих к некоторому следствию эквивалентна комплексной причине следствия («Если есть дружба, и она крепкая, то это надолго» ≡ «Если есть крепкая дружба, то это надолго»
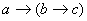 ≡
≡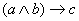 ). И наоборот, комплексная причина эквивалентна цепи следующих друг за другом причин
). И наоборот, комплексная причина эквивалентна цепи следующих друг за другом причин 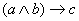 ≡
≡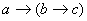 . Однако эта часть правила требует осторожности, так как, пользуясь ей, не следует забывать о временной последовательности цепи причин из-за которой, разложение комплексной причины на цепь последовательных не всегда применимо. Так, например, нельзя перестроить суждение «Вода и свет порождают жизнь» в суждение «Вода порождает свет, в свою очередь, порождающий жизнь»; суждение «Если есть крепкая дружба, то это надолго» можно ошибочно перестроить в «Если есть крепкая и она – дружба, то это надолго» и, тем самым, получить бред душевнобольного, понять который, возможно только зная исходный текст. Но имеются суждения, которым позволено использовать данное правило без ограничений: «Верить и ждать, значит надеяться» ≡ «Ждать, значит верить, значит, надеяться».
. Однако эта часть правила требует осторожности, так как, пользуясь ей, не следует забывать о временной последовательности цепи причин из-за которой, разложение комплексной причины на цепь последовательных не всегда применимо. Так, например, нельзя перестроить суждение «Вода и свет порождают жизнь» в суждение «Вода порождает свет, в свою очередь, порождающий жизнь»; суждение «Если есть крепкая дружба, то это надолго» можно ошибочно перестроить в «Если есть крепкая и она – дружба, то это надолго» и, тем самым, получить бред душевнобольного, понять который, возможно только зная исходный текст. Но имеются суждения, которым позволено использовать данное правило без ограничений: «Верить и ждать, значит надеяться» ≡ «Ждать, значит верить, значит, надеяться».
Эти правила позволяют, в случае необходимости, перестраивать суждения, не нарушая их смысл.
Правила отрицания
Простые суждения легко отрицать полностью, методом внешнего опровержения («Не верно что, мыслительные способности нарастают по мере взросления») или частично, методом внутреннего отрицания («Многие люди не стремятся мыслить разумно»). Сложные суждения, образованные конъюнкцией, отрицать так же легко («Не правильно называть тех, кто видит в жизни преобладание негативных сторон, как и тех, кто видит преобладание позитивных – реалистами» и «Здравомыслие включает в себя элемент творчества, а не веру в предопределенность»). Еще легче отрицать отрицательные суждения, как правило, для этого достаточно убрать из них отрицание. Однако отрицание некоторых суждений может вызвать затруднения, избежать которых помогут правила отрицания, логически следующие из правил эквивалентности:
 ;
;  ;
; 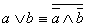 ;
; 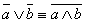 ;
; 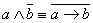 .
.
Перестроив по этому правилу суждение в модальное опровержение, легко, убрав оператор опровержения, или вынеся его за двоеточие, превратить суждение в его противоположность. Например, для отрицания суждения «Он или толстый или короткий» можно преобразовать его в эквивалентное модальное суждение «Не верно что, он не толстый и не короткий», а затем вынести «неверно», получив модальное «Неверно: он не толстый и не короткий» или ассерторическое «Он не толстый и не короткий».
< Глава 2 Глава 3 Глава 4. >
