
| КрасносельскийКонстантинКонстантинович |

 Компьютер и программы
Компьютер и программы

 WEB-дизайн
WEB-дизайн

 Литература и поэзия
Литература и поэзия

 Гуманитарные науки
Гуманитарные науки

 Логика
Логика

 Альтернативная логика
Альтернативная логика
 Введение
Введение
 Глава 1. Законы правильного мышления
Глава 1. Законы правильного мышления
 Глава 2. Способы познания
Глава 2. Способы познания
 Глава 3. Суждение (высказывание).
Глава 3. Суждение (высказывание).
 Глава 4. Умозаключения.
Глава 4. Умозаключения.
 Глава 5. Простые умозаключения (силлогизмы).
Глава 5. Простые умозаключения (силлогизмы).
 Глава 6. Простой категорический силлогизм.
Глава 6. Простой категорический силлогизм.
 Глава 7. Полисиллогизм.
Глава 7. Полисиллогизм.
 Глава 8. Методы оптимизации мышления
Глава 8. Методы оптимизации мышления
 Глава 9. Аналогия
Глава 9. Аналогия
 Глава 10. Индукция
Глава 10. Индукция
 Глава 11. Интуиция
Глава 11. Интуиция
 Глава 12. Мышление и его ошибки
Глава 12. Мышление и его ошибки
 Глава 13. Построение теорий
Глава 13. Построение теорий
 Глава 14. Теория аргументации
Глава 14. Теория аргументации
 Глава 15. Основы риторики
Глава 15. Основы риторики
 Глава 16. Практика риторики
Глава 16. Практика риторики
 Заключение
Заключение

 Психология
Психология

 Эрих Фромм
Эрих Фромм

 Иметь или быть?
Иметь или быть?
 Вступительная статья
Вступительная статья
 Предисловие
Предисловие
 Введение
Введение
Часть I
 Глава I. Первый взгляд
Глава I. Первый взгляд
 Глава II. Обладание и бытие в повседневной жизни
Глава II. Обладание и бытие в повседневной жизни
 Глава III. Обладание и бытие в Ветхом и Новом завете и в трудах Майстера Экхарта
Глава III. Обладание и бытие в Ветхом и Новом завете и в трудах Майстера Экхарта
Часть II
 Глава IV. Что такое модус обладания?
Глава IV. Что такое модус обладания?
 Глава V. Что такое модус бытия?
Глава V. Что такое модус бытия?
 Глава VI. Другие аспекты обладания и бытия: безопасность – опасность
Глава VI. Другие аспекты обладания и бытия: безопасность – опасность
Часть III
 Глава VII. Религия, характер и общество
Глава VII. Религия, характер и общество
 Глава VIII. Условия изменения человека и черты нового человека
Глава VIII. Условия изменения человека и черты нового человека
 Глава IX. Черты нового общества новая наука о человеке
Глава IX. Черты нового общества новая наука о человеке

 Человек для себя
Человек для себя
 Предисловие
Предисловие
 Глава I. Проблема
Глава I. Проблема
 Глава II. Гуманистическая этика: прикладная наука искусства жить
Глава II. Гуманистическая этика: прикладная наука искусства жить
 Глава III. Человеческая природа и характер
Глава III. Человеческая природа и характер
 Глава IV. Проблемы гуманистической этики
Глава IV. Проблемы гуманистической этики
 Глава V. Моральная проблема нашего времени
Глава V. Моральная проблема нашего времени
 Послесловие. Разумность добра
Послесловие. Разумность добра

 Психоанализ и религия
Психоанализ и религия
 Предисловие
Предисловие
 Фрейд и Юнг
Фрейд и Юнг
 Анализ некоторых типов религиозного опыта
Анализ некоторых типов религиозного опыта
 Психоаналитик - «врачеватель души»
Психоаналитик - «врачеватель души»
 Психоанализ - угроза для религии?
Психоанализ - угроза для религии?
 Примечания
Примечания

 Искусство любить
Искусство любить
 Предисловие
Предисловие
 Является ли любовь искусством?
Является ли любовь искусством?
 Теория любви
Теория любви
 Объекты любви
Объекты любви
 Любовь и ее распад в современном обществе
Любовь и ее распад в современном обществе
 Практика любви
Практика любви

 Психические болезни. Справочник
Психические болезни. Справочник
 Аффективные синдромы
Аффективные синдромы
 Алкоголизм
Алкоголизм
 Амнестический (корсаковский) синдром
Амнестический (корсаковский) синдром
 Бредовые синдромы
Бредовые синдромы
 Дефект психический
Дефект психический
 Галлюцинаторный синдром (галлюциноз)
Галлюцинаторный синдром (галлюциноз)
 Истерический синдром
Истерический синдром
 Интоксикационные психозы
Интоксикационные психозы
 Кататонические синдромы
Кататонические синдромы
 Маниакально-депрессивный психоз
Маниакально-депрессивный психоз
 Навязчивые состояния (обсессии)
Навязчивые состояния (обсессии)
 Неврозы
Неврозы
 Олигофрения
Олигофрения
 Прогрессивный паралич
Прогрессивный паралич
 Помрачение сознания
Помрачение сознания
 Пресенильные (предстарческие, инволюционные) психозы
Пресенильные (предстарческие, инволюционные) психозы
 Психопатии
Психопатии
 Психоорганический синдром (органический психосиндром)
Психоорганический синдром (органический психосиндром)
 Реактивные психозы
Реактивные психозы
 Сенестопатически-ипохондрический синдром
Сенестопатически-ипохондрический синдром
 Сенильные психозы (старческие психозы)
Сенильные психозы (старческие психозы)
 Симптоматические психозы
Симптоматические психозы
 Сверхценные идеи
Сверхценные идеи
 Токсикомании и наркомании
Токсикомании и наркомании
 Травматическая энцефалопатия
Травматическая энцефалопатия
 Шизофрения
Шизофрения
 Эпилепсия
Эпилепсия

 История
История

 История упадка Римской империи
История упадка Римской империи
 Введение
Введение
 Империя во время язычества
Империя во время язычества
 Установление христианства в качестве государственной религии
Установление христианства в качестве государственной религии
 Империя во время правления династии Константина
Империя во время правления династии Константина
 Империя при Валентиниане и Валенте
Империя при Валентиниане и Валенте
 Империя при Феодосии Великом
Империя при Феодосии Великом
 Империя под управлением детей Феодосия
Империя под управлением детей Феодосия
 Поход Алариха в Италию
Поход Алариха в Италию
 Итоги
Итоги
 Причины падения Западной Римской Империи
Причины падения Западной Римской Империи
 Как и когда древние люди научились добывать огонь?
Как и когда древние люди научились добывать огонь?
 Средневековое мракобесие и современная наука древней Греции
Средневековое мракобесие и современная наука древней Греции
 Существовал ли Иисус?
Существовал ли Иисус?
 Любовь
Любовь
 Понятие веры в Исповеди Толстого
Понятие веры в Исповеди Толстого
 Отупление отменяется
Отупление отменяется
 И другое...
И другое...

 Мастерская
Мастерская
 Хронология материалов
Хронология материалов
 Обращение к посетителям
Обращение к посетителям
 Скачать шрифты
Скачать шрифты
 Скачать рефераты
Скачать рефераты
 Создание web сайта на заказ
Создание web сайта на заказ
 Создание веб сайтов (цены)
Создание веб сайтов (цены)
 Веб-сайты, созданные мной (потенциальным заказчикам)
Веб-сайты, созданные мной (потенциальным заказчикам)
 Полезные ссылки
Полезные ссылки
 Об авторе
Об авторе
 Статистика сайта
Статистика сайта


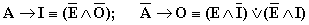



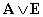 либо только одно суждение истинно, либо оба суждения ложны (например: «Либо все люди – негры (1), либо не один человек не негр (2)»), а в сложном разделительном суждении типа
либо только одно суждение истинно, либо оба суждения ложны (например: «Либо все люди – негры (1), либо не один человек не негр (2)»), а в сложном разделительном суждении типа  одно суждение обязательно истинно (например: «Либо все птицы летают (1), либо некоторые из них не летают (2)»). В сложном суждении типа
одно суждение обязательно истинно (например: «Либо все птицы летают (1), либо некоторые из них не летают (2)»). В сложном суждении типа 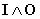 оба простых суждения могут быть одинаково истинными, хотя одно из них, может оказаться ложным («Некоторые люди счастливы (1), в то время, когда некоторые, несчастны (2)»).
оба простых суждения могут быть одинаково истинными, хотя одно из них, может оказаться ложным («Некоторые люди счастливы (1), в то время, когда некоторые, несчастны (2)»).
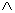
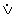 ) неверно что ни одна рыба не дышит легкими (
) неверно что ни одна рыба не дышит легкими (